
Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.
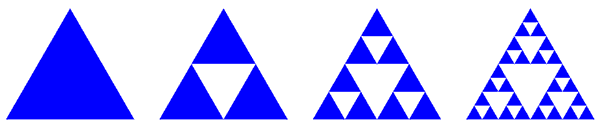
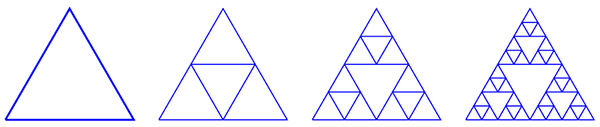
Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.
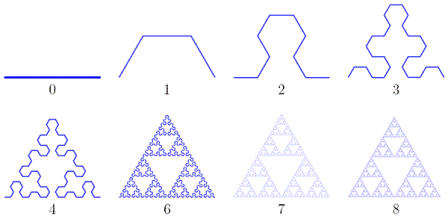
Следующий способ получить треугольник Серпинского еще больше похож на обычную схему построения геометрических фракталов с помощью замены частей очередной итерации на масштабированный фрагмент. Здесь на каждом шаге составляющие ломаную отрезки заменяются на ломаную из трех звеньев (она сама получается в первой итерации). Откладывать эту ломаную нужно попеременно то вправо, то влево. Видно, что уже восьмая итерация очень близка к фракталу, и чем дальше, тем ближе будет подбираться к нему линия.
Но и на этом не всё. Оказывается, треугольник Серпинского получается в результате одной из разновидностей случайного блуждания точки на плоскости. Этот способ называется «игрой Хаос». С его помощью можно построить и некоторые другие фракталы.
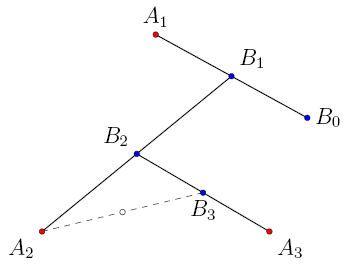
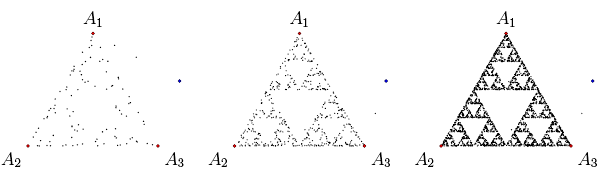
Суть «игры» такова. На плоскости зафиксирован правильный треугольник A1 A2 A3. Отмечают любую начальную точку B0. Затем случайным образом выбирают одну из трех вершин треугольника и отмечают точку B1 — середину отрезка с концами в этой вершине и в B0 (на рисунке справа случайно выбралась вершина A1). То же самое повторяют с точкой B1, чтобы получить B2. Потом получают точки B3, B4, и т. д. Важно, чтобы точка «прыгала» случайным образом, то есть чтобы каждый раз вершина треугольника выбиралась случайно, независимо от того, что было выбрано в предыдущие шаги. Удивительно, что если отмечать точки из последовательности Bi, то вскоре начнет проступать треугольник Серпинского. Ниже изображено, что получается, когда отмечено 100, 500 и 2500 точек.
Некоторые свойства
Фрактальная размерность log23 ≈ 1,584962... . Треугольник Серпинского состоит из трех копий самого себя, каждая в два раза меньше. Взаимное расположение их таково, что если уменьшить клеточки сетки в два раза, то число квадратиков, пересекающихся с фракталом, утроится. То есть N(δ/2) = 3N(δ). Если сначала размер клеток был 1, а с фракталом пересекалось N0 из них (N(1) = N0), то N(1/2) = 3N0, N(1/4) = 32N0, ..., N(1/2k) = 3kN0. Отсюда получается, что N(δ) пропорционально 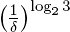 , и по определению фрактальной размерности она равна как раз log23.
, и по определению фрактальной размерности она равна как раз log23.
- Треугольник Серпинского имеет нулевую площадь. Это означает, что в фрактал не влезет ни один, даже очень маленький, кружок. То есть, если отталкиваться от построения первым способом, из треугольника «вынули» всю внутренность: после каждой итерации площадь того, что остается, умножается на 3/4, то есть становится всё меньше и стремится к 0. Это не строгое доказательство, но другие способы построения могут только усилить уверенность, что это свойство всё-таки верно.
- Неожиданная связь с комбинаторикой. Если в треугольнике Паскаля с 2n строками покрасить все четные числа белым, а нечетные — черным, то видимые числа образуют треугольник Серпинского (в некотором приближении).
Варианты
Ковер (квадрат, салфетка) Серпинского. Квадратная версия была описана Вацлавом Серпинским в 1916 году. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т. д.

Как и у треугольника, у квадрата нулевая площадь. Фрактальная размерность ковра Серпинского равна log38, вычисляется аналогично размерности треугольника.
Пирамида Серпинского. Один из трехмерных аналогов треугольника Серпинского. Строится аналогично с учетом трехмерности происходящего: 5 копий начальной пирамиды, сжатой в два раза, составляют первую итерацию, ее 5 копий составят вторую итерацию, и т. д. Фрактальная размерность равна log25. У фигуры нулевой объем (на каждом шаге половина объема выбрасывается), но при этом площадь поверхности сохраняется от итерации к итерации, и у фрактала она такая же, как и у начальной пирамиды.

Губка Менгера. Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log320. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.


