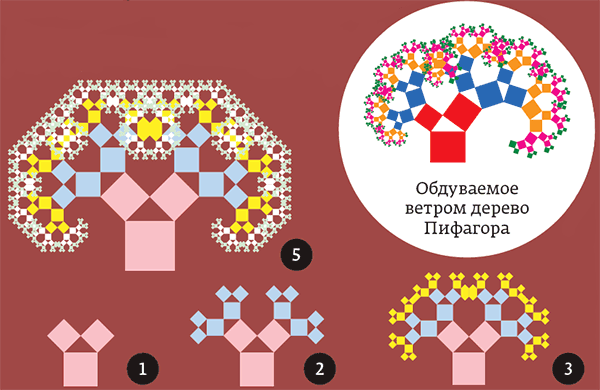
Называется так потому, что каждая тройка попарно соприкасающихся квадратов ограничивает прямоугольный треугольник и получается картинка, которой часто иллюстрируют теорему Пифагора — пифагоровы штаны во все стороны равны.

Хорошо видно, что всё дерево ограничено. Если самый большой квадрат единичный, то дерево поместится в прямоугольник 6 × 4. Значит, его площадь не превосходит 24. Но с другой стороны, каждый раз добавляется в два раза больше троек квадратиков, чем в предыдущий, а их линейные размеры в √2 раз меньше. Поэтому на каждом шаге добавляется одна и та же площадь, которая равна площади начальной конфигурации, то есть 2. Казалось бы, тогда площадь дерева должна быть бесконечна! Но на самом деле противоречия здесь нет, потому что довольно быстро квадратики начинают перекрываться, и площадь прирастает не так быстро. Она всё-таки конечна, но, по всей видимости, до сих пор точное значение неизвестно, и это открытая проблема.

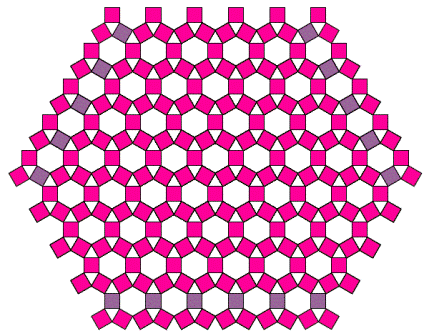
Если менять углы при основании треугольника, то будут получаться немного другие формы дерева. А при угле 60° все три квадрата окажутся равными, а дерево превратится в периодический узор на плоскости:

Можно даже заменять квадраты на прямоугольники. Тогда дерево будет больше похоже на настоящие деревья.

А при некоторой художественной обработке получаются весьма реалистичные изображения: